Home matrix re

Image feature of matrix Re{ˆRRe{ˆ Re{ˆR R R}. From top to bottom, θ =

By A Mystery Man Writer
Last updated 29 Jun 2024
Image feature of matrix Re{ˆRRe{ˆ Re{ˆR R R}. From top to bottom, θ =
Image feature of matrix Re{ˆRRe{ˆ Re{ˆR R R}. From top to bottom, θ =
Framework of the proposed simple estimation CNN.
Image feature of matrix Re{ˆRRe{ˆ Re{ˆR R R}. From top to bottom, θ =
PDF) Multi-DOA Estimation Based on the KR Image Tensor and
Image feature of matrix Re{ˆRRe{ˆ Re{ˆR R R}. From top to bottom, θ =
Solved Find the standard matrix for the linear
Image feature of matrix Re{ˆRRe{ˆ Re{ˆR R R}. From top to bottom, θ =
Solved The matrix operators corresponding to rotations Rx(θ
Image feature of matrix Re{ˆRRe{ˆ Re{ˆR R R}. From top to bottom, θ =
Linear Algebra 10: Computing a basis for the image of a matrix
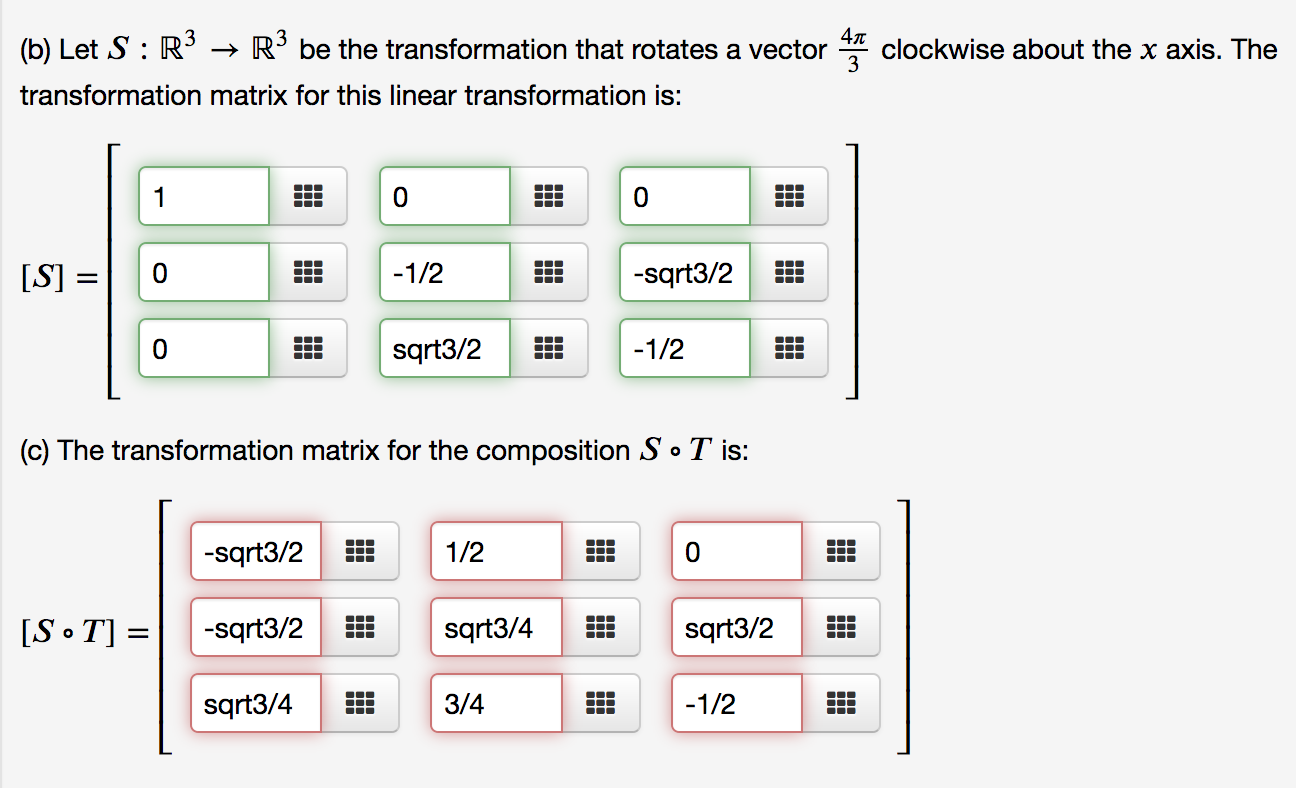
Image feature of matrix Re{ˆRRe{ˆ Re{ˆR R R}. From top to bottom, θ =
Solved (9 points) When rotating about a coordinate axis
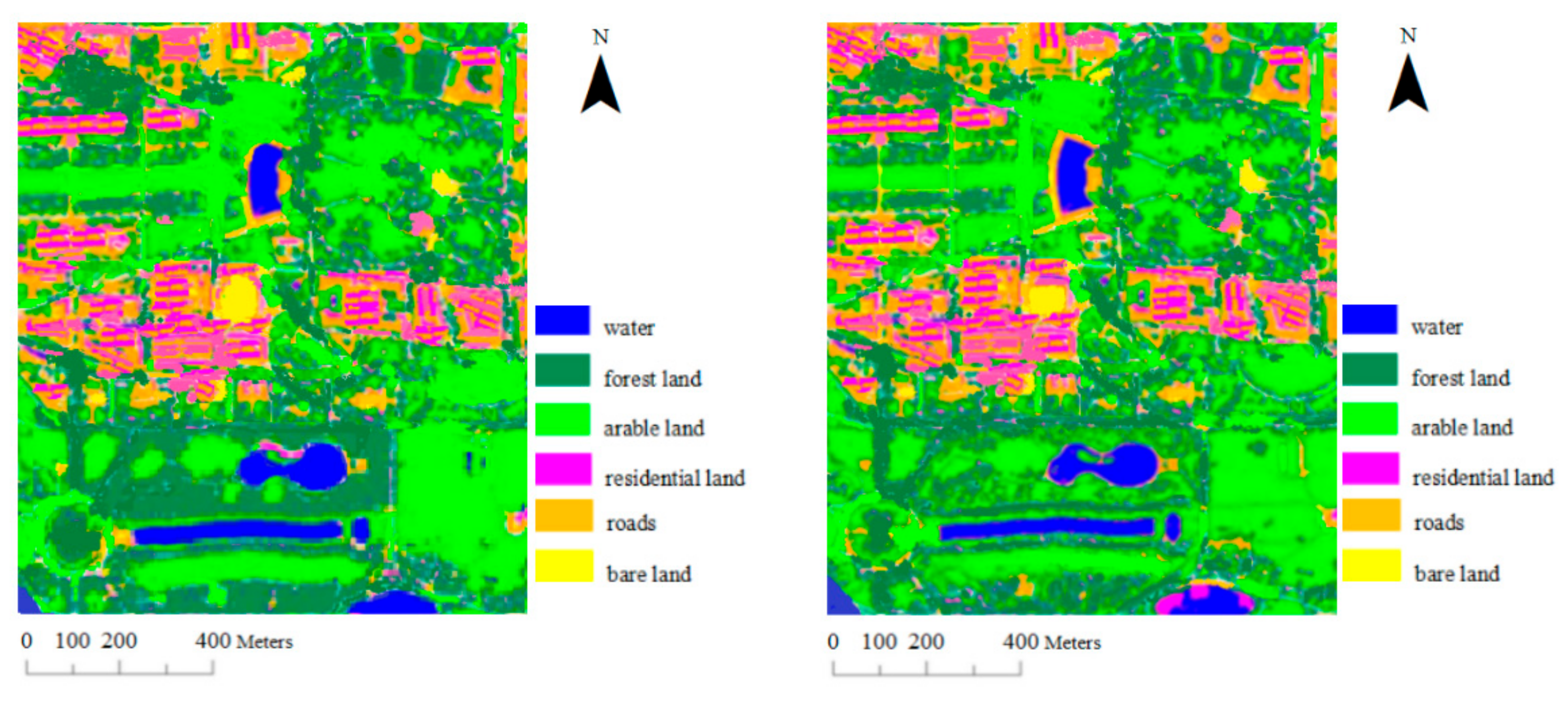
Image feature of matrix Re{ˆRRe{ˆ Re{ˆR R R}. From top to bottom, θ =
Sensors, Free Full-Text
Image feature of matrix Re{ˆRRe{ˆ Re{ˆR R R}. From top to bottom, θ =
8 6b image of points under linear transformation
Image feature of matrix Re{ˆRRe{ˆ Re{ˆR R R}. From top to bottom, θ =
8 6b image of points under linear transformation
Image feature of matrix Re{ˆRRe{ˆ Re{ˆR R R}. From top to bottom, θ =
Solved Consider the rotation matrix R = [cos theta sin theta
Image feature of matrix Re{ˆRRe{ˆ Re{ˆR R R}. From top to bottom, θ =
Low-rank matrix regression for image feature extraction and
Image feature of matrix Re{ˆRRe{ˆ Re{ˆR R R}. From top to bottom, θ =
Image feature of matrix Re{ˆRRe{ˆ Re{ˆR R R}. From top to bottom
Recommended for you
You may also like

© 2014-2024 itak-shop.ir. Inc. or its affiliates.